Viernes, 02 de Diciembre del 2016
Clase #14
Miércoles, 07 de Diciembre del 2016
Eventos Independientes
Algunas situaciones de probabilidad implican más de un evento. Cuando los eventos no se afectan entre sí, se les conoce como eventos independientes. Los eventos independientes pueden incluir la repetición de una acción como lanzar un dado más de una vez, o usar dos elementos aleatorios diferentes, como lanzar una moneda y girar una ruleta.
Sean A y B eventos cualesquiera de un espacio muestral S. Se dice que A y B son independientes si
P(A|B) = P(A) y P(B|A) = P(B)
Si A y B son eventos independientes, P(A y B) = P(A) • P(B).
En general, para cualquier número de eventos independientes, la probabilidad de que todos los eventos sucedan es el producto de las probabilidades de que sucedan los eventos individuales. |
Para complementar el tema con ejercicios resueltos puedes hacer click en la siguiente imagen
Probabilidad Total
Llamamos sistema completo de sucesos a una familia de sucesos A1, A2, ...,An que cumplen:
- Son incompatibles dos a dos, Ai
 Aj = Ø
Aj = Ø - La unión de todos ellos es el suceso seguro,

Sea A1, A2, ...,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai), entonces la probabilidad del suceso B viene dada por la expresión:
Clase #15
Viernes, 09 de Diciembre del 2016
En esta clase realizamos varios ejercicios sobre Probabilidad, aplicando los conceptos adquiridos en la anteriores clases, se presentaron ejercicios utilizando distintos métodos de resolución y así logramos concluir cuál es más eficiente para cada tipo de problema.
Ejemplo de Ejercicio realizado en clase:
En un juego de 40 se reparten 5 cartas al azar a cada jugada a partir de un mato de 40 cartas. ¿Cuál es la probabilidad de que jugador tenga:
a.- Un as, un dos, un tres, un cuatro, un cinco del mismo palo
b.- 4 cartas del mismo palo
c.- Una ronda (3 cartas iguales)
Al resolverlos notamos la poca probabilidad que existe de que ocurran estos sucesos en este conocido juego
Segundo Bimestre
Clase #1
Miércoles, 14 de Diciembre del 2016
Variables Aleatorias Discretas
Una variable discreta es aquella que solo puede tomar un número finito de valores entre dos valores cualesquiera de una característica.
Las Variables Aleatorias establecen correspondencia del espacio muestral S al conjunto de los números reales. Esta correspondencia es funcional y se la puede definir formalmente.
Definición: Variable aleatoria
- Sean X: Variable aleatoria
- S: Espacio muestral
- e: Cualquier elemento de S
- x: Valor que puede tomar X
- R: Conjunto de los números reales
Entonces
X: S → R Es la correspondencia que establece la variable aleatoria X
e → x, dom X = S, rg X ⊂ R
Ejemplo:
En un experimento se lanzan tres monedas y se observa el resultado (c: cara o s: sello).
El conjunto de posibles resultados (espacio muestral) para este experimento, es el siguiente:
Describa con una variable, el número de sellos que se obtienen.
Los posibles resultados se los puede representar con una variable. Si X es ésta variable, entonces se dice que X es una variable aleatoria:
Al realizar el experimento, se obtendrá cualquier elemento del espacio muestral S.
Por lo tanto, la variable aleatoria X puede tomar alguno de los números:
x = 0, 1, 2, 3.
Tabule la correspondencia que establece la variable aleatoria X del ejemplo anterior:
Las variables aleatorias pueden representarse con las letras mayúsculas X, Y, ...
Para un mismo espacio muestral S pueden definirse muchas variables aleatorias.
Para el ejemplo de las 3 monedas, algunas otras variables aleatorias sobre S pueden ser:
Sea X una variable aleatoria discreta cuyos valores suponemos ordenados de menor a mayor. Llamaremos función de distribución de la variable X, y escribiremos F(x) a la función:
e → x, dom X = S, rg X ⊂ R
Ejemplo:
En un experimento se lanzan tres monedas y se observa el resultado (c: cara o s: sello).
El conjunto de posibles resultados (espacio muestral) para este experimento, es el siguiente:
S = {( c, c, c),( c, c, s),( c, s, c),( s, c, c),( c, s, s),( s, c, s),( s, s, c),( s, s, s)}
Describa con una variable, el número de sellos que se obtienen.
Los posibles resultados se los puede representar con una variable. Si X es ésta variable, entonces se dice que X es una variable aleatoria:
X: Variable aleatoria (número de sellos que se obtienen)
Al realizar el experimento, se obtendrá cualquier elemento del espacio muestral S.
Por lo tanto, la variable aleatoria X puede tomar alguno de los números:
x = 0, 1, 2, 3.
Tabule la correspondencia que establece la variable aleatoria X del ejemplo anterior:
Las variables aleatorias pueden representarse con las letras mayúsculas X, Y, ...
Para un mismo espacio muestral S pueden definirse muchas variables aleatorias.
Para el ejemplo de las 3 monedas, algunas otras variables aleatorias sobre S pueden ser:
Y: Diferencia entre el número de caras y sellos
Z: El número de caras al cubo, mas el doble del número de sellos, etc.
Para cada variable aleatoria el rango es un subconjunto de los reales. Según el tipo de correspondencia establecida, las variables aleatorias pueden ser discretas o continuas.
En el ejemplo de las monedas, X es una variable aleatoria discreta pues su rango es un subconjunto de los enteros. Además es finita.
Z: El número de caras al cubo, mas el doble del número de sellos, etc.
Para cada variable aleatoria el rango es un subconjunto de los reales. Según el tipo de correspondencia establecida, las variables aleatorias pueden ser discretas o continuas.
En el ejemplo de las monedas, X es una variable aleatoria discreta pues su rango es un subconjunto de los enteros. Además es finita.
Propiedades de la Distribución de Probabilidad de una Variable Aleatoria Discreta
Sean X: Variable aleatoria discreta
f(x): Distribución de Probabilidad de X
Propiedades de f(x)
1) ∀x [ f(x) ≥ 0 ] Los valores de probabilidad no pueden ser negativos
2) ∑f(x) 1 = La suma de todos los valores de probabilidad es 1
x
x
Función distribución de probabilidad
Sea X una variable aleatoria discreta cuyos valores suponemos ordenados de menor a mayor. Llamaremos función de distribución de la variable X, y escribiremos F(x) a la función:
Ejemplo:
Se utilizan para variables continuas o para variables discretas, con un gran número de datos, y que se han agrupado en clases.
En el eje abscisas se construyen unos rectángulos que tienen por base la amplitud del intervalo, y por altura, la frecuencia absoluta de cada intervalo.
La superficie de cada barra es proporcional a la frecuencia de los valores representados.
Función distribución de probabilidad acumulada
La función de distribución asocia a cada valor de la variable aleatoria la probabilidad acumulada hasta ese valor.
Ejemplo:
Media y Varizanza de las variables aleatorias discretas
Media
El Valor Esperado o Media es una medida estadística que describe la tendencia central de una variable aleatoria. Podemos pensar que representa el valor promedio que tomaría la variable aleatoria si el experimento se realizara un gran número de veces en condiciones similares.Varianza
Variables aleatorias continuas
Una variable aleatoria X es continua si su función de distribución es una función continua.En la práctica, se corresponden con variables asociadas con experimentos en los cuales la variable medida puede tomar cualquier valor en un intervalo: mediciones biométricas, intervalos de tiempo, áreas, etc.
Función de densidad de Probabilidad
La probabilidad de una variable aleatoria continua puede especificarse si existe una función
denominada función de densidad de probabilidad (o simplemente función de densidad), talque el área debajo del gráfico de esta función cumpla los requisitos para que sea una medida
del valor de probabilidad. Para variables aleatorias discretas, la probabilidad se obtiene de la
sumatoria de f(x). En el límite, esta sumatoria se transforma en un integral.
Definición: Función de Densidad de Probabilidad
Sea X una variable aleatoria continua.
Se dice que f es una función de densidad de probabilidad si y solo si,
Miércoles, 21 de Diciembre del 2016
Al igual que en el caso discreto se puede definir una función de probabilidad acumulada, la cual en el caso continuo se denomina función de distribución
Función de Distribución
Sea X una variable aleatoria contínua con función de densidad f(x)
Entonces, la función
se denomina función de distribución de la variable aleatoria X
Propiedades de la Función de Distribución
Puedes encontrar ejercicios resueltos sobre las variables aleatorias continuas dando click en el siguiente link:


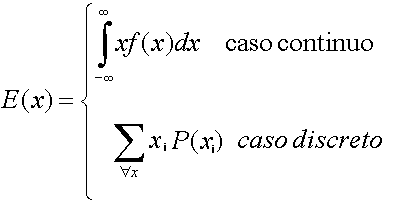



No hay comentarios:
Publicar un comentario