Clase #4
Miércoles, 04 de Enero del 2017
Propiedades
Puedes encontrar más información sobre la media y la varianza de las variables aleatorias continuas dando click en la siguiente imagen:
Distribuciones de Probabilidad Discretas
Tenemos esta distribución cuando el resultado de una experiencia aleatoria puede ser un conjunto finito de n posibles resultados, todos ellos igualmente probables.
Un ejemplo puede ser la variable X, puntuación en el lanzamiento de un dado regular. Esta variable toma seis valores posibles, todos con la misma probabilidad p = 1/6. La función de densidad de esta variable será:
f(k) = P[X = k] = 1/6 k = 1, 2, 3, 4, 5, 6
Propiedades del modelo Uniforme discreto
Sea n el número de valores equiprobables posibles:
1) Esperanza:
2) Varianza:
Distribución Bernoulli
La distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito ( ) y valor 0 para la probabilidad de fracaso
) y valor 0 para la probabilidad de fracaso
( ).Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro P.
).Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro P.
Distribución Binomial
La distribución Binomial es una distribución de probabilidad discreta que mide el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una Probabilidad fija p de ocurrencia del éxito entre los ensayos.
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad Q = 1 - p. En la distribución Binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para N = 1, la Binomial se convierte, de hecho, en una distribución de Bernoulli.
N= Numero de eventos.
X= Numero de éxitos.
P= Probabilidad de éxito.
Q= probabilidad de fracaso.
F(X)= Probabilidad de tener X éxitos en un numero N de ensayos.
Clase #5
Viernes, 06 de Enero del 2017
Distribución Binomial
Media: n.p
Clase #6
Miércoles, 11 de Enero del 2017
Distribución de Poisson
Como vemos, este modelo se caracteriza por un sólo parámetro λ, que debe ser positivo.
Esta distribución suele utilizarse para contajes del tipo número de individuos por unidad de tiempo, de espacio, etc.
Propiedades del modelo de Poisson
1) Esperanza: E(X) = λ.
2) Varianza: V(X) = λ.
En esta distribución la esperanza y la varianza coinciden.
3) La suma de dos variables aleatorias independientes con distribución de Poisson resulta en una nueva variable aleatoria, también con distribución de Poisson, de parámetro igual a la suma de parámetros:
X1 ~ P(λ = λ1) y X2 ~ P(λ = λ2)
y definimos Z = X1 + X2, entonces,
Z ~ P(λ = λ1 + λ2)
Este resultado se extiende inmediatamente al caso de n variables aleatorias independientes con distribución de Poisson. En este caso, la variable suma de todas ellas sigue una distribución de Poisson de parámetro igual a la suma de los parámetros.
Puedes encontrar ejercicios resueltos sobre la definición de Poisson dando click en el siguiente link:
http://www.blogupiicsa.com/2010/12/distribucion-de-poisson_04.htmlClase #7
Viernes, 13 de Enero del 2017
Distribución Hipergeométrica
Esta distribución se refiere a los experimentos estadísticos que consisten en tomar una
muestra sin reemplazo, de un conjunto finito el cual contiene algunos elementos considerados “éxitos” y los restantes son considerados “fracasos”.Tomar una muestra sin reemplazo significa que los elementos son tomados uno a uno, sin
devolverlos. Podemos concluir entonces que los ensayos ya no pueden ser considerados
independientes porque la probabilidad de “éxito” al tomar cada nuevo elemento es afectada por el resultado de los ensayos anteriores debido a que la cantidad de elementos de la población está cambiando.
Distribución Binomial Negativa
Este modelo de probabilidad tienen características similares al modelo binomial: los ensayos
son independientes, cada ensayo tiene únicamente dos resultados posibles, y la probabilidad
que cada ensayo tenga un resultado favorable es constante. Pero, en este modelo la variable
aleatoria es diferente:
En la Distribución Binomial Negativa, la variable de interés es la cantidad de ensayos que se
realizan hasta obtener un número requerido de éxitos, k
Media y Varianza
Distribución Geométrica
Media y Varianza
Puedes encontrar ejercicios resueltos de estas funciones de distribución dando click en el siguiente link:
Clase #8
Miércoles, 18 de Enero del 2017
Distribuciones de Probabilidad Continuas
Distribución Uniforme
Este modelo corresponde a una variable aleatoria continua cuyos valores tienen igual valor de probabilidad en un intervalo específico para la variable
se define por la siguiente función de probabilidad:
Su gráfica se representa de la siguiente manera:
Esperanza de la función uniforme continua
Varianza de la función uniforme continua
de donde 
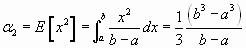
por lo que 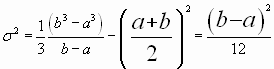
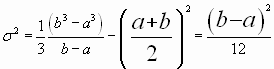
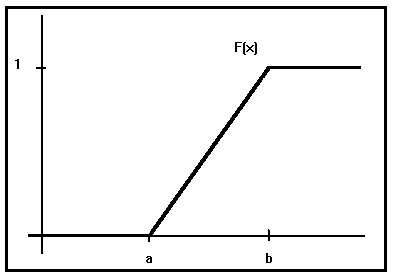
Función de distribución acumulada:

Su representación gráfica será :
Distribución Normal
Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa por N(μ, σ), si se cumplen las siguientes condiciones:1. La variable puede tomar cualquier valor: (-∞, +∞)
2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:
Curva de la distribución normal
- El campo de existencia es cualquier valor real, es decir, (-∞, +∞).
- Es simétrica respecto a la media µ.
- Tiene un máximo en la media µ.
- Crece hasta la media µ y decrece a partir de ella.
- En los puntos µ − σ y µ + σ presenta puntos de inflexión.
- El eje de abscisas es una asíntota de la curva.
Caso Especial
Distribución Normal Estándar
La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ = 0, y por desviación típica la unidad, σ =1.
Su función de densidad es:
Su gráfica es:
La probabilidad de la variable X dependerá del área del recinto sombreado en la figura. Y para calcularla utilizaremos una tabla.
Para poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).
Estas probabilidades nos dan la función de distribución Φ(k).
Φ(k) = P(z ≤ k)
Búsqueda en la tabla de valor de k
Unidades y décimas en la columna de la izquierda.
Céntesimas en la fila de arriba.
P(Z ≤ a)

P(Z ≤ 1.47) = 0.9292
P(Z > a) = 1 - P(Z ≤ a)

P(Z > 1.47) = 1 − P(Z ≤ 1.47) = 1 − 0.9292 = 0.0708
Unidades y décimas en la columna de la izquierda.
Céntesimas en la fila de arriba.
P(Z ≤ a)
P(Z ≤ 1.47) = 0.9292
P(Z > a) = 1 - P(Z ≤ a)
P(Z > 1.47) = 1 − P(Z ≤ 1.47) = 1 − 0.9292 = 0.0708
Tabla de la distribución Normal Estándar: http://www.vitutor.com/pro/5/a_3.html
Ejercicios de la Distribución Normal: http://www.vitutor.com/pro/5/a_g.html
Clase #9
Viernes, 20 de Enero del 2017
Viernes, 20 de Enero del 2017
En esta clase se rindió la tercera prueba del semestre sobre funciones de distribución discretas
Clase #10
Miércoles, 25 de Enero del 2017
Valores referenciales a la función normal
La probabilidad equivale al área encerrada bajo la curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %
Aproximación de la Distribución Binomial con la Distribución Normal
n · p ≥ 5 y n · q ≥ 5.
La distribución binomial B(n, p) se puede aproximar mediante una distribución normal:


Ejemplo:En una ciudad una de cada tres familias posee teléfono. Si se eligen al azar 90 familias, calcular la probabilidad de que entre ellas haya por lo menos 30 tengan teléfono.




Clase #11
Viernes, 27 de Enero del 2017
Distribución Exponencial
Una de las distribuciones de variable continua más importantes es la distribución exponencial la cual se utiliza como modelo para representar el tiempo de funcionamiento o de espera. Tiene como función expresar también el tiempo transcurrido entre eventos que se contabilizan por medio de la distribución de Poisson. Un ejemplo de esto podría ser el tiempo que transcurre entre dos llamadas por teléfono, número de peatones que llegan a un semáforo, etc.





La distribución binomial B(n, p) se puede aproximar mediante una distribución normal:
Ejemplo:En una ciudad una de cada tres familias posee teléfono. Si se eligen al azar 90 familias, calcular la probabilidad de que entre ellas haya por lo menos 30 tengan teléfono.
Después de la clase de realizó la Corrección de la Evaluación del día viernes que la podrás encontrar en Evidencias
Clase #11
Viernes, 27 de Enero del 2017
Distribución Exponencial
Una de las distribuciones de variable continua más importantes es la distribución exponencial la cual se utiliza como modelo para representar el tiempo de funcionamiento o de espera. Tiene como función expresar también el tiempo transcurrido entre eventos que se contabilizan por medio de la distribución de Poisson. Un ejemplo de esto podría ser el tiempo que transcurre entre dos llamadas por teléfono, número de peatones que llegan a un semáforo, etc.
La función de densidad o ley de probabilidad es:
siendo λ el parámetro de la distribución con λ>0.
Como Propiedades tenemos que:
Toda variable aleatoria continua que sigue una norma de distribución exponencial posee las siguientes características,
• El valor esperado es,
Aquel Valor cuya probabilidad de que sea tomado por una variable dada es máxima.
• La varianza es,
La esperanza del cuadrado de la desviación de dicha variable respecto a su media o valor esperado.
La gráfica de la función de distribución exponencial

La Función de Distribución Acumulada
La gráfica de la Función de Distribución Acumulada

Relación entre las distribuciones Exponencial y PoissonSea x la variable que cuenta el número de eventos que ocurren en el tiempo (0,t), con media "λt", entonces
Sea T el tiempo que transcurre hasta que sucede el primer evento Poisson, el rango de T es [0, + ∞) y su función de distribución
donde:
El evento (T>t) indica el primer evento Poisson ocurre después de t, es decir (T>t) = (x=0)







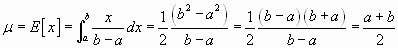



No hay comentarios:
Publicar un comentario